11 min to read
자바 8 인 액션
13. 함수형 관점으로 생각하기

시스템 구현과 유지보수
보통 유지보수 과정에서 코드 크래시 디버깅 문제를 많이 겪게 되는데 이는 예상치 못한 변수값의 발생에 의한 경우가 많다.
하지만, 함수형 프로그래밍은 side effect를 줄여주고 불변성이라는 개념을 통해 이러한 문제를 해결해 줄 수 있다.
공유된 가변 데이터
변수가 예상치 못한 값을 갖는 이유는 결국 우리가 유지보수하는 시스템의 여러 메서드에서 공유된 가변 데이터 구조를 읽고 갱신하기 때문이다. 공유 가변 데이터 구조를 사용하면 프로그램 전체에서 데이터 갱신 사실을 추적하기 어려워진다.
선언형 프로그래밍
어떻게(how)에 집중하는 프로그래밍 형식을 명령형 프로그래밍이라고 부른다.
무엇을에 집중하는 방식은 선언형 프로그래밍이라고 부르기도 한다. 선언형 프로그래밍은 내부 반복을 통해 질의문 자체러 문제를 풀어나간다. 이것이 내부 반복 프로그래밍의 장점이다. 선언형 프로그래밍에서는 우리가 원하는 것이 무엇이고 시스템이 그 목표를 달성할 것인지 등의 규칙을 정한다. 문제 자체가 코드로 명확하게 드러난다는 점이 선언형 프로그래밍의 강점이다.
왜 함수형 프로그래밍인가?
함수형 프로그래밍은 선언형 프로그래밍을 따르는 대표적인 방식이며 앞서 설명한 바와 같이 부작용이 없는 계산을 지향한다. 선언형 프로그래밍과 부작용을 멀리한다는 두 가지 개념은 좀 더 쉽게 시스템을 구현하고 유지보수하는데 도움을 준다.
람다 표현식을 활용하면 작업을 조합하거나 동작을 전달하는 방식인 선언형을 활용하여 자연스럽고 읽고 쓸 수 있는 코드를 구현하는 데 많은 도움을 준다.
스트림으로는 여러 연산을 연결해서 복잡한 질의를 표현할 수 있다.
이러한 기능들이 함수형 프로그래밍의 특징을 나타낸다.
따라서 함수형 프로그래밍을 이용하면 부작용이 없는 복잡하고 어려운 기능을 구현할 수 있다.
함수형 프로그래밍이란 무엇인가?
함수형 프로그래밍에서 함수란 수학적인 함수와 같다. 즉, 0개 이상의 인수를 가지며 한 개 이상의 결과를 반호나하지만 부작용이 없어야 한다. 함수는 여러 입력을 받아서 여러 출력을 생성하는 블랙박스와 같다.
즉, 함수 그리고 if-then-else 등의 수학적인 표현만 사용하는 방식을 순수 함수형 프로그래밍이라고 하며 시스템의 다른 부분에 영향을 미치지 않는다면 내부적으로는 함수형이 아닌 기능도 사용하는 방식을 함수형 프로그래밍이라 한다.
함수형 자바
실질적으로 자바로는 완벽한 순수 함수형 프로그래밍을 구현하기 어렵다. 따라서 자바에서는 순수 함수형이 아닌 함수형 프로그램을 구현한다. 실제 부작용이 있지만 아무도 이를 보지 못하게 함으로써 함수형을 달성할 수 있다.
예를 들자면, 부작용을 일으키지 않는 어떤 함수네 메서드가 있는데, 다만 진입할 때 어떤 필드의 값을 증가시켰다가 빠져나올 때 필드의 값을 돌려놓는다고 가정한다.
단일 스레드로 실행되는 프로그램의 입장에서는 이 메서드가 아무 부작용을 일으키지 않으므로 이 메서드는 함수형이라 간주할 수 있지만 다른 스레드가 필드의 값을 확인한다거나 동시에 이 메서드를 호출하는 상황이 발생한다면 이 메서드는 함수형이 아니다.
메서드의 바디를 lock을 걸어 함수형으로 해결할 수는 있지만 멀티코어 프로세서의 두 코어를 활용해서 메서드를 병렬로 호출할 수가 없게 된다.
즉, 프로그램 입장에서 부작용이 사라졌지만 프로그래머 관점에서는 프로그램의 실행 속도가 느려지게 된 것이다.
함수나 메서드는 지역 변수만 변경해야 함수형이라 할 수 있다. 그리고 함수나 메서드에서 참조하는 객체가 있다면 그 객체는 불변 객체여야 한다. 즉, 객체의 모든 필드가 final이어야 하고 모든 참조 필드는 불변 객체를 직접 참조해야 한다.
단, 예외적으로 메서드 내에서 생성한 객체의 필드는 갱신할 수 있다. 다만 새로 생성한 객체의 필드 갱신이ㅣ 외부에 노출되지 않아야 하고 다음에 메서드를 다시 호출한 결과에 영향을 미치지 않아야 한다.
이 외에도 함수형이려면 함수나 메서드가 어떤 예외도 일으키지 않아야 한다. 예외가 발생한다면 블랙박스 모델에서 return으로 결과를 반환할 수 없게 되기 때문이다. 이러한 제약은 함수형을 수학적으로 활용하는 데 큰 걸림돌이 될 것이다.
마지막으로 함수형에서는 비함수형 동작을 감출 수 있는 상황에서만 부작용을 포함하는 라이브러리를 사용해야 한다. 즉, 먼저 자료구조를 복사한다거나 발생할 수 있는 예제를 적절하게 내부적으로 처리함으로써 자료구조의 변경을 호출자가 알 수 없도록 감춰야 한다.
이와 같은 설명을 주석 혹은 어노테이션으로 메서드를 정의할 수 있다.
우리가 만든 함수형 코드에서는 일종의 로그 파일로 디버깅 정보를 출력하도록 구현하는 것이 좋다. 물론 이처럼 디버깅 정보를 출력하는 것은 함수형의 규칙에 위배되지만 로그 출력을 제외하고는 함수형 프로그래밍의 장점을 문제없이 누릴 수 있다.
참조 투명성
‘부작용을 감춰야 한다.’라는 제약은 참조 투명성(referential transparency)개념으로 귀결된다. 즉, 같은 인수로 함수를 호출했을 때 항상 같은 결과를 반환한다면 참조적으로 투명한 함수라고 표현한다. 다시 말해 함수는 어떤 입력이 주어졌을 때 언제, 어디서 호출하든 같은 결과를 생성해야 한다.(따라서 Random.nextInt는 함수형이 될 수 없다.)
참조 투명성은 프로그램 이해에 큰 도움을 준다. 또한 참조 투명성은 비싸거나 오랜 시간이 걸리는 연산을 기억화또는 캐싱을 통해 다시 계산하지 않고 저장하는 최적화 기능도 제공한다.
자바에서는 참조 투명성과 관련한 작은 이슈가 있다. List를 반환하는 메서드를 두 번 호출할때, 두 번의 호출 결과는 같은 요소지만 다른 메모리 공간에 생성된 리스트를 참조하게 된다.
결과 리스트가 가변 객체라면(반환된 두 리스트가 같은 객체라 할 수 없으므로) 리스트를 반환하는 메서드는 참조적으로 투명한 메서드가 아니라는 결론이 나온다. 하지만 결과 리스트를 (불변의) 순수 값으로 사용할 것이라면 두 리스트가 같은 객체가 아니더라도 같은 객체라 간주함으로써 해당 함수는 참조적으로 투명한 것이라고 간주 할 수 있다.
일반적으로 함수형 코드에서는 이런 함수를 참조적으로 투명한 것으로 간주한다.
객체지향 프로그래밍과 함수형 프로그래밍
사실 자바 8에서는 함수형 프로그래밍을 익스트림 객체지향 프로그래밍의 일종으로 간주한다. 대부분의 자바 개발자는 무의식적으로 함수형 프로그래밍의 일부 기능과 익스트림 객체지향 프로그래밍의 일부 기능을 사용하게 될 것이다.
함수형 실전 연습
- 모든 서브집합 출력
static List<List<Integer>> insertAll(Integer first, List<List<Integer>> lists) {
List<List<Integer>> result = new ArrayList<>();
for (List<Integer> list : lists) {
List<Integer> copyList = new ArrayList<>();
copyList.add(first);
copyList.addAll(list);
result.add(copyList);
}
return result;
}
static List<List<Integer>> concat(List<List<Integer>> subans, List<List<Integer>> subans2) {
// 1.
subans.addAll(subans2);
// 2.
List<List<Integer>> r = new ArrayList<>(subans);
r.addAll(subans2);
return subans;
}
static List<List<Integer>> subsets(List<Integer> list) {
if (list.isEmpty()) {
List<List<Integer>> ans = new ArrayList<>();
ans.add(Collections.emptyList());
return ans;
}
Integer first = list.get(0);
List<Integer> rest = list.subList(1, list.size());
List<List<Integer>> subans = subsets(rest);
List<List<Integer>> subans2 = insertAll(first, subans);
return concat(subans, subans2);
}
public static void main(String[] args) {
List<Integer> list = Arrays.asList(1, 4, 9);
subsets(list).stream().forEach(System.out::println);
}
insertAll 함수를 함수형으로 만들기 위해 호출자가 아닌 insertAll 내부에서 리스트를 복사하여 코드를 추가하였다.
static concat 함수에서는 1번보다 2번 처럼 구현하는 것이 바람직하다.
2번의 concat은 순수 함수다. 내부적으로는 리스트 r에 요소를 추가하는 변화가 있지만 반환 결과는 오직 인수에 의해 이뤄지며 인수 정보는 변경되지 않는다.
반면에 1번은 concat(subans, subans2) 호출 시 subans의 값을 다시 참조하지 않는다는 가정이 있어야 한다.
실제 예제에서는 subans 값을 다시 참조하지 않기 때문에 개발자는 상황에 따라 2번과 같이 더 가볍게 concat 함수를 사용할 지, 아니면 잠재적인 버그를 찾기 위해 시간을 소비하는 것이 비용이 적을 지 고려해서 사용해야 한다.
재귀와 반복
순수 함수형 프로그래밍 언어에서는 while, for 같은 반복문을 포함하지 않는다. 왜냐하면 이러한 반복문에 의해 변화가 자연스럽게 코드에 스며들 수 있기 때문이다.
- 반복문이 아닌 iterator를 활용한 예시
Iterator<Apple> it = apples.iterator();
while(it.hasNext()) {
Apple apple = it.next();
...
}
위 코드에서는 호출자가 변화를 확인할 수 없으므로 아무 문제가 없다.
- for-each 루프를 사용하는 예시
public void searchForGold(List<String> l, Stats stats) {
for (String s : l) {
if ("gold".equals(s)) {
stats.incrementFor("gold");
}
}
}
루프 내부에서 프로그램의 다른 부분과 공유되는 stats 객체의 상태를 변화시키게 되면서 문제가 발생할 수 있다.
따라서 이러한 문제때문에 순수 함수형 프로그래밍 언어에서는 부작용 연산을 원천적으로 제거하기 위해 재귀를 이용한다. 재귀를 이용하면 루프 단계마다 갱신되는 반복 변수를 제거할 수 있다.
- 반복 방식의 팩토리얼
static int factorialIterative(int n) {
int r = 1;
for (int i = 1; i <= n; i++) {
r *= i;
}
return r;
}
반복 방시의 팩토리얼은 매 반복마다 변수 r과 i가 갱신된다.
- 재귀 방식의 팩토리얼
static long factorialRecursive(long n) {
return n == 1 ? 1 : n * factorialRecursive(n - 1);
}
재귀 방식은 함수 내에서 변수가 갱신되는 것이 아닌, 좀 더 수학적인 형식으로 문제를 해결한다.
- 스트림 팩토리얼
static long factorialStreams(long n) {
return LongStream.rangeClosed(1, n)
.reduce(1, (a, b) -> a * b);
}
효율성 측면에서 봤을 때 함수형 프로그래밍의 장점이 분명하긴 하지만 주의해야 할 점이 있다.
일반적으로 반복 코드보다 재귀 코드가 더 cost가 비싸다. 왜냐하면 재귀 함수를 호출할 때 마다 생성되는 정보를 저장할 새로운 스택 프레임이 만들어지게 되면서 재귀 팩토리얼 입력 값에 비례하여 메모리 사용량이 증가하게 된다. 따라서 너무 큰 입력값을 입력하게 되면 StackOverflowError가 발생한다.
그러면 재귀는 사용하지 못하는 방식일까? 함수형 언어에서는 꼬리 호출 최적화(tail-call optimization)라는 해결책을 제공한다.
- 꼬리 재귀 팩토리얼
static long factorialTailRecursive(long n) {
return factorialHelper(1, n);
}
static long factorialHelper(long acc, long n) {
return n == 1 ? acc : factorialHelper(acc * n, n - 1);
}
factorialHelper에서 재귀 호출이 가장 마지막에서 이뤄지게 된다. 반면, 이전의 factorialRecursive에서 마지막으로 수행한 연산은 n과 재귀 호출의 결과 값의 곱이다.
중간 결과를 각각의 스택 프레임으로 저장해야 하는 일반 재귀와 달리 꼬리 재귀는 컴파일러가 하나의 스택 프레임을 재활용할 수 있게 된다.
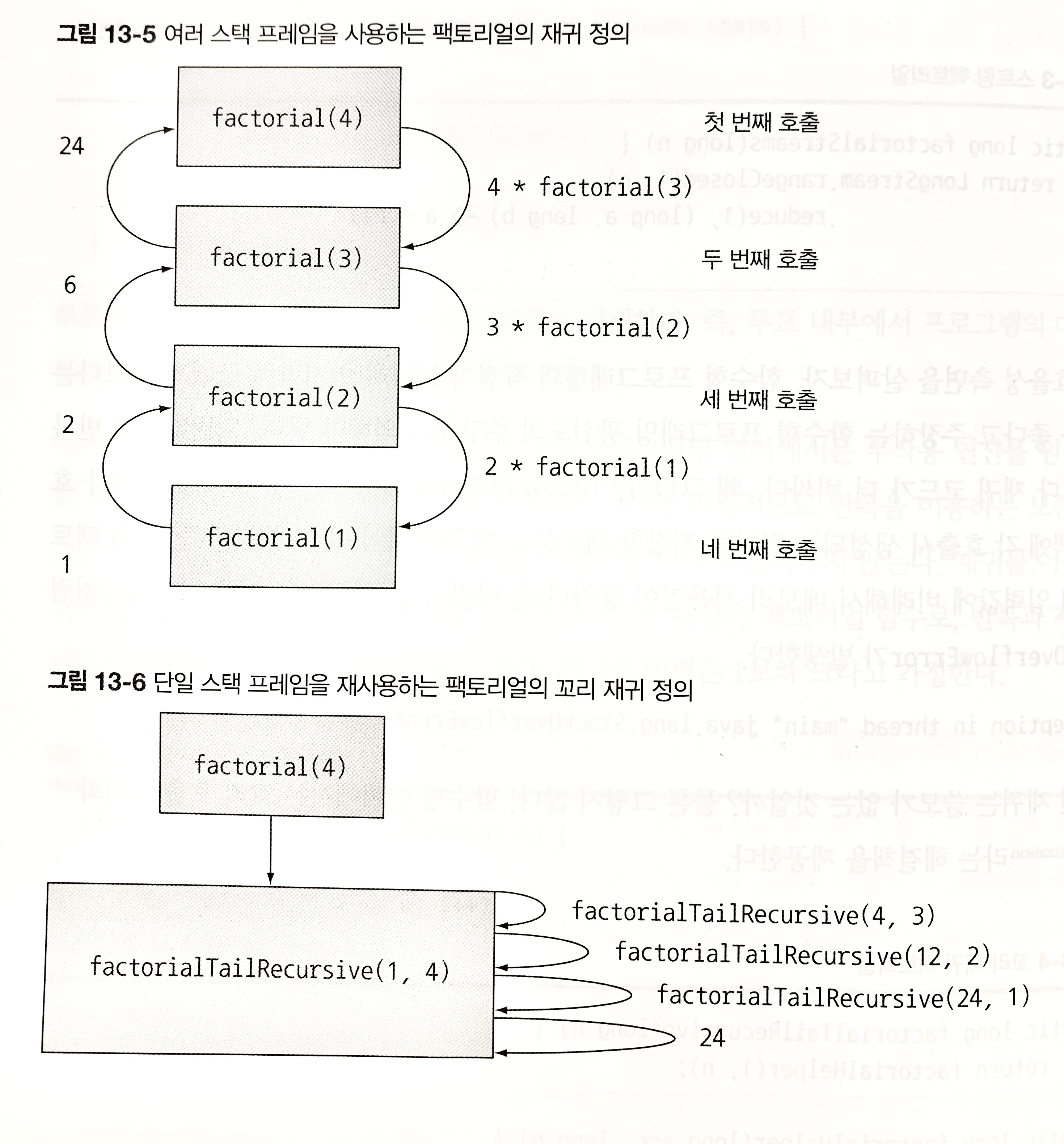
안타깝게도 자바는 이와 같은 최적화를 제공하지 않는다. 그럼에도 여러 컴파일러 최적화 여지를 남겨둘 수 있는 꼬리 재귀를 적용하는 것이 좋다. 스칼라, 그루비 같은 최신 JVM 언어는 이와 같은 재귀를 반복으로 변환하는 최적화를 제공한다.(속도 손실 없이)
결과적으로 순수 함수형을 유지하면서도 유용성뿐 아니라 효율성까지 두 마리의 토끼를 모두 잡을 수 있다.
결론적으로 자바 8에서는 반복을 스트림으로 대체해서 변화를 피할 수 있다. 또한 반복을 재귀로 바꾸면 더 간결하고 부작용이 없는 알고리즘을 만들 수 있다. 실제로 재귀를 이용하면서 좀 더 쉽게 읽고, 쓰고 이해할 수 있는 예제를 만들 수 있다. 또한 약간의 실행시간의 차이보다는 개발자의 효율성이 더 중요할 때도 많다.
요약
- 공유된 가변 자료구조를 줄이는 것은 장기적으로 프로그램을 유지보수하고 디버깅하는데 도움이 된다.
- 함수형 프로그래밍은 부작용이 없는 메서드와 선언형 프로그래밍 방식을 지향한다.
- 함수형 메서드는 입력 인수와 출력 결과만을 갖는다.
- 같은 인수 값으로 함수를 호출했을 때 항상 같은 값을 반환하면 참조 투명성을 갖는 함수다. while 루프 같은 반복문은 재귀로 대체할 수 있다.
- 자바에서는 고전 방식의 재귀보다는 꼬리 재귀(or stream)를 사용해야 추가적인 컴파일러 최적화를 기대할 수 있다.

Comments